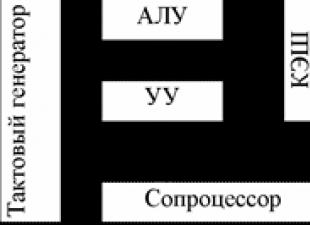
MATLAB дахь тооцоолол ба өгөгдлийн ойролцоо

Шугаман алгебрийн тэгшитгэлийн систем, спектрийн бодлого бодох

Шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх нь тооцооллын гол асуудлуудын нэг юм, учир нь олон төрлийн хэрэглээний талбарт үүссэн асар олон тооны асуудлыг үүнд багасгадаг. Механик асуудлын ойролцоо шийдэл, шингэн ба хийн урсгалыг тооцоолоход ашигладаг тоон аргууд, тасралтгүй орчин дахь бусад физик процессууд, цахилгаан хэлхээг тооцоолох арга, өгөгдлийг ойролцоогоор тооцоолох аргууд нь шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх хэрэгцээнд хүргэдэг. Энэ нь шугаман алгебрийн системийн үүсэх эх сурвалжуудын бүрэн жагсаалт биш юм). Жишээлбэл, бүтцийн давтамжийн шинжилгээ, цахилгаан хэлхээ, хяналтын систем дэх үйл явцын тогтвортой байдлыг судлах болон бусад олон салбарт спектрийн асуудлууд үүсдэг.

Шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх MATLAB-ын боломжуудын тойм

MATLAB орчин нь анх матрицтай ажиллахад зориулагдсан (MATLAB нь Матрицын лаборатори гэсэн үгийн товчлол) тул шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх MATLAB хэрэгслүүдийн арсенал нэлээд баялаг бөгөөд дараахь зүйлийг агуулна.

• дөрвөлжин ба тэгш өнцөгт матрицтай системийг шийдвэрлэх;
• системийг шууд ба давталтын (урьдчилсан нөхцөлийг бүрдүүлэх боломжийг оруулаад) аргаар шийдвэрлэх;
• матрицын задрал;
• том сийрэг матрицуудыг авсаархан хэлбэрээр хадгалах, ийм матрицтай системийг шийдвэрлэх тусгай алгоритмууд.

Эсрэг ташуу зураас ашиглан системийг шийдвэрлэх

Системийг шийдэх хамгийн энгийн арга бол урвуу зураасыг ашиглах явдал юм. Бид системийг шийдэх хэрэгтэй гэж бодъё

Үүнийг хийхийн тулд баруун талд матриц болон баганын векторыг бөглөнө үү (баруун тал нь багана байх ёстой, эс тэгвээс хэмжээсүүдийн таарахгүй байдлын талаархи алдаа гарч ирнэ)

мөн урвуу ташуу зураасыг ашиглана уу

X = A\f x = 1 1 1

Буруу ташуу тэмдгийн оронд та mldivide функцийг дуудаж болно

X = ml хуваах(A, f)

Үр дүн нь адилхан байх болно

Зөрчлийг тооцоолсноор бид шийдлийг зөв олсон эсэхийг шалгана (ерөнхийдөө, зөрүүтэй бүрэлдэхүүн хэсгүүдийн жижиг утгууд нь зөв олдсон шийдлийг үргэлж заадаггүй)

F - A*x ans = 0 0 0

А, f хоёрыг холихгүй байх нь маш чухал, учир нь мэс засал хийх үед

ямар ч алдаа гарахгүй, гэхдээ энэ нь харагдах болно

X = 0.2707 0.3439 0.3854

Энэ нь авч үзэж буй системийн шийдэлтэй ямар ч холбоогүй юм. "Матриц" f ба "баруун тал" А-тай системийг бичих замаар яагаад ийм зүйл болдгийг харцгаая. Энэ тохиолдолд зөвхөн нэг үл мэдэгдэх зүйл байх болно, учир нь f хэмжээ 3-аас 1:

Хэрэв баруун талд матриц байгаа бол матрицын багана байгаатай адил олон системийг шийдэх бөгөөд багана бүр нь харгалзах системийн баруун талын вектор юм (өөрөөр хэлбэл, урвуу ташуу зураасны оператор нь хэд хэдэн асуудлыг шийдэх боломжийг танд олгоно. системүүд нэг дор). Тиймээс системүүд шийдэгдсэн

Хатуухан хэлэхэд эдгээр системүүдийн аль нь ч шийдэлгүй. Гэсэн хэдий ч, хэрэв системийн матриц нь тэгш өнцөгт бөгөөд түүний эгнээний тоо нь баганын тооноос их байвал (жишээлбэл, тэгшитгэлийн тоо нь үл мэдэгдэх тооноос их) байвал ийм системийг хэт тодорхойлогдсон систем ба түүний ойролцоо гэж нэрлэдэг. үлдэгдлийн Евклидийн нормыг багасгах замаар шийдлийг хайж байна. Тиймээс эхний системийн хувьд шийдэл нь байх болно x, энэ нь дараах илэрхийлэлд хамгийн бага хэмжээг өгдөг

(4-7х 1) 2 +(3-11х 1) 2 +(2-12х 1) 2

Хамгийн бага нь зөвхөн . Жишээлбэл, Symbolic Math Toolbox-ийг ашиглая

Syms x R = (7*x-4)^2 + (11*x-3)^2 + (12*x-2)^2 dRdx = ялгаа(R) x = шийдвэрлэх(dRdx) x = 85/314 давхар(x) ans = 0.2707

Тэгэхээр x = f\A гэж бичих замаар олж авсан вектор нь тус бүрийн баруун тал нь А матрицын харгалзах багана болох хэт тодорхойлогдсон гурван системийн шийдийг агуулна.

Мэдээж хэрэг дарагдсан системийн матриц нь зөвхөн нэг багана байх албагүй. Жишээ болгон параметр сонгох асуудлыг авч үзье аТэгээд бшугаман загвар өгөгдсөн хүснэгтийн мэдээллийн дагуу

к	1	2	3	4	5
х к	1.0	1.5	2.0	2.5	3.0
у к	2.99	2.81	2.89	3.03	3.21

Энэ асуудал нь хэт тодорхойлогддог систем рүү буурдаг аТэгээд б, хэрэв бид тэгш байдлыг шаардах юм бол у(х к)=у кУчир нь к=1,2,...,5:

Бид системийн матриц ба баруун талын векторыг бүрдүүлдэг

X = (1:0.5:3)" A = ; f = ; мөн үүнийг шийднэ c = A\f бид c = 2.9903 2.0100 олж авна, өөрөөр хэлбэл өгөгдөл ба ойролцоо тооцооллын график нь олж авсан үр дүнгийн үнэн зөвийг баталж байна fun = @ (x) ) c(1)/x + c(2)*log(x); fplot(хөгжилтэй, ) талбай дээр барих(x, y, "эсвэл")

Хэрэв систем нь үл мэдэгдэхээс олон тэгшитгэлтэй бол ийм системийг дутуу тодорхойлогдоогүй систем гэж нэрлэх ба MATLAB дээр урвуу зураасаар шийдэж болно. Энэ нь хязгааргүй олон шийдэлтэй байх бөгөөд аль болох олон тэг утгыг агуулсан шийдэл олддог. Энэ жишээг авч үзье

A = ; f = ; x = A\f x = 1.3333 1.0000 0 1.6667

Урвуу зураасын тэмдэгтээс гадна ердийн ташуу зураасыг бас ашигладаг. Тэд дараах дүрмээр холбогддог

B/A нь (A"\B")"-тай тэнцүү
апостроф нь шилжүүлэг гэсэн утгатай. Энгийн налуу зураасны оронд та mrdivide функцийг ашиглаж болно.

Одоохондоо бид урвуу зураасын үйлдэлд суулгагдсан системийг шийдвэрлэх алгоритмуудыг судлахгүй. Энэ хэсэг нь үүнд зориулагдсан болно. Ялангуяа LU задралыг ерөнхий квадрат матрицтай системийг шийдвэрлэхэд ашигладаг. Үүнээс гадна матрицын нөхцөл байдлыг шалгана. Нөхцөл байдал муутай матрицын сонгодог жишээ бол элементүүдийг томъёогоор тодорхойлдог Хилберт матриц юм. MATLAB дээр өгөгдсөн хэмжээтэй Хилберт матрицыг үүсгэхийн тулд hilb функцийг ашиглана. Жишээлбэл, 13-р эрэмбийн системийг шийдье, баруун гар тал нь түүний шийдэл нь бүх нэгж байх ёстой ( кБаруун талын 3-р элемент нь элементүүдийн нийлбэр юм к- матрицын р эгнээ). A = hilb(13); f = нийлбэр(A, 2); x = A\f

Үүний үр дүнд бид муу агааржуулалтын тухай мессеж хүлээн авдаг

Анхааруулга: Матриц нь дан хэмжээтэй ойрхон эсвэл муу масштабтай байна. Үр дүн буруу байж магадгүй. RCOND = 2.339949e-018.

(RCOND бол нөхцлийн тоон урвуу утгын тооцоолол) ба буруу шийдэл

X = 1.0000 1.0000 1.0004 0.9929 1.0636 0.6552 2.2023 -1.7860 5.3352 -3.4773 3.9431 -0.1145 1.1851

Матрицыг муу нөхцөлдүүлснээс үүсэх аюулыг энэ хэсэгт тайлбарласан болно. Одоо бид MATLAB дээр байдаг матрицын задралын тойм руу шилжиж байна.

Cholesky, LU болон QR матрицын задрал

MATLAB нь дараах өргөтгөлүүдэд зориулагдсан функцтэй.

• Cholesky өргөтгөл - функц chol;
• LU өргөтгөл - функц lu;
• QR задрал - qr функц.

Өргөтгөл нь ижил матрицтай, баруун талын хэд хэдэн вектор бүхий шугаман алгебрийн тэгшитгэлийн бүхэл бүтэн системийг үр дүнтэй шийдвэрлэхэд тусалдаг. Дараах багц системийг авч үзье.

Ax=f(k), к=1, 2,...,Н.

матриц гэж үзье Ань хоёр матриц, матрицтай системүүдийн үржвэр хэлбэрээр илэрхийлэгддэг A=BCболон матрицтай системүүд БТэгээд Cматрицаас хамаагүй хурдан шийддэг А. Дараа нь анхны системүүдийн шийдлүүдийг дараах байдлаар олж авна. Учир нь Ax=f(k)Тэгээд A=BC, Тэр BCx=f (к)ба дараалан шийдвэрлэх By=f(k)Тэгээд Cx=yбид шийдлийг олдог к th систем. Дүүргэгдсэн матрицын хувьд задралыг дараах байдлаар гүйцэтгэнэ. О(n 3) үйл ажиллагаа хаана n- матрицын хэмжээ (жишээ нь системийг шийдэхтэй ижил хугацаанд), өргөтгөлийн хүчин зүйл тус бүрээр системийг шийдвэрлэх. О(n 2) үйл ажиллагаа. Тиймээс шийдэл Нсистем c урьдчилсан өргөтгөл авдаг О(n 3)+О(n 2)Н. Систем бүрийг матрицын задралгүйгээр шийдэх нь шаардлагатай болно О(n 3)Нарифметик үйлдлүүд.

Өгөгдсөн матрицын хувьд Cholesky задрал Аийм дээд гурвалжин матрицыг олохоос бүрдэнэ Рэерэг диагональ элементүүдтэй, аль нь A=R T R. Энэ нь мэдэгдэж байгаа бол матриц Атэгш хэмтэй ба эерэг тодорхой (жишээ нь аливаа векторын хувьд xүнэн бол: x T Ax0, эсвэл ижил, матрицын бүх хувийн утга эерэг), тэгвэл Чолескийн задрал байдаг бөгөөд өвөрмөц юм.

Холескийн матрицын задралыг жишээ болгон авч үзье

A = ; R = chol(A) R = 2.0000 0.5000 0.5000 0 1.9365 0.3873 0 0 1.8974

Энгийн шалгалт нь задаргаа зөв хийгдсэн эсэхийг баталгаажуулдаг (бодит тоон дээр ажиллах явцад гарсан алдааны нарийвчлалын хүрээнд)

A - R"*R ans = 1.0e-015 * 0 0 0 0 0 0 0 0 0 0.4441

Хэрэв матриц эерэг тодорхой биш бол энэ нь задралын явцад тодорхой болно, учир нь сөрөг тооны үндсийг задлах шаардлагатай бөгөөд холбогдох анхааруулга гарч ирнэ.

A = ; R = chol(A)??? ==> chol матрицыг ашиглах алдаа нь эерэг тодорхойлогдсон байх ёстой.

Chol функц нь матрицын тэгш хэмийг шалгадаггүй. Тооцоололд диагональ ба түүнээс дээш хэсэгт байрлах анхны матрицын элементүүдийг ашигладаг.

A = ; R = chol(A) R = 2.0000 0.5000 1.0000 0 1.9365 0.2582 0 0 1.7127 A - R"*R ans = 0 0 0 0 0 0 -1 0 0

Дурын квадрат матрицын хувьд үүнийг хийж болно Л.У.- задрал, өөрөөр хэлбэл. доод гурвалжин матрицыг ол Лба дээд гурвалжин матриц Утиймэрхүү A=LU. Илүү хатуу мэдэгдлийг дараах байдлаар томъёоллоо.

Хэрэв Ак- квадрат матрицын үндсэн минор Ахэмжээ n, эхнийхээс эмхэтгэсэн кмөр ба багана (жишээ нь: A(1:k, 1:k)) болон det( А к)0 хувьд к=1,2,..., n-1, тэгвэл өвөрмөц доод гурвалжин матриц байна Л, диагональ нь нэгээс бүрдэх ба цорын ганц дээд гурвалжин матриц Утиймэрхүү A=LU.

Тооцоолох үед Л.У.Өргөтгөх процессын тоон тогтвортой байдлыг хангахын тулд LU өргөтгөл нь эгнээ солих шаардлагатай байж болох тул lu функц нь матрицыг буцаана. Л, эгнээ солих хүртэл доод гурвалжин, жишээ нь:

A = ; = lu(A) L = 0 1.0000 0 1.0000 0 0 0.5000 0.5000 1.0000 U = 2 3 1 0 1 1 0 0 4

Ажил Л.У.Хаана Л- эгнээнүүдийг солих хүртэл гурвалжин байх ба матрицтай тэнцүү байх болно А(ерөнхийдөө бодит тоонуудтай үйлдлийн алдааг харгалзан).

A-L*U ans = 0 0 0 0 0 0 0 0 0

Хэрэв матрицын хувьд АХэрэв Cholesky задрал эсвэл LU задрал хийгдсэн бол матрицтай системийн шийдэл. А, дээр дурдсанчлан гурвалжин матрицтай хоёр системийг шийдэхэд хүрдэг. Энэ шийдлийг буцааж ташуу зураасыг ашиглан хийж болно, учир нь түүний ард байгаа алгоритм нь гурвалжин матрицуудыг тодорхойлж, тэдгээрийн тусламжтайгаар системийг шийдвэрлэх үр дүнтэй аргыг ашигладаг. О(n 2) арифметик үйлдлүүд. Системийг шийдэх жишээг авч үзье

урьдчилсан байдлаар Л.У.- матрицын задрал.

A = ; f = ;

Бид гүйцэтгэдэг Л.У.- задрал

Лу(А);

гурвалжин матрицтай хоёр системийг эхлээд L, дараа нь U гэсэн дарааллаар шийднэ

Y = L\f; x = U\y x = 1 1 1

Хоёр системийн шийдлийг нэг илэрхийллээр бичиж болно

X = U\(L\f)

мөн үр дүн нь ижил байх болно. Гурвалжин матрицтай системийн шийдлийн дарааллыг тодорхойлохын тулд хаалт ашиглахын ач холбогдлыг анхаарч үзэх хэрэгтэй. Хаалтгүй илэрхийлэл

X = U\L\f

эхлээд гүйцэтгэсэн тул огт өөр үр дүнд хүргэнэ U\L, энэ нь U матриц ба L баганатай системийг баруун талын вектор болгон шийдвэрлэхтэй тэнцүү (дээр дурдсанчлан). Үр дүн нь багана бүр нь харгалзах системийн шийдэл болох матриц бөгөөд дараа нь энэ матриц болон баруун талын вектор f системээр шийдэгдэнэ. Энэ процесс нь анхны системийн шийдэлтэй ямар ч холбоогүй нь ойлгомжтой.

Сүүлийн матрицын задралыг авч үзье - QR-qr функцээр гүйцэтгэсэн задрал. QR-Тэгш өнцөгт матрицын хувьд задралыг хийж болно, нарийн бол Ахэмжээ матриц мдээр n, тэгвэл ортогональ матриц байна Qхэмжээ мдээр м(өөрөөр хэлбэл Q -1 =Q T байхаар) ба матриц Рхэмжээ мдээр nүндсэн диагональ дор бүх тэг элементүүдтэй, аль A=QR.

QR- Өргөтгөл нь тооцооллын тогтвортой байдал сайтай бөгөөд ялангуяа хамгийн бага квадратын аргыг ашиглан өгөгдлийг ойролцоолоход ашиглагддаг. Жишээлбэл, QR задралыг ашиглан өмнөх системийг шийдэх талаар авч үзье.

Qr(A) Q = -0.7428 0.6000 -0.2971 -0.5571 -0.8000 -0.2228 -0.3714 0.0000 0.9285 R = -5.3852 -5.3852 -5.0138 0000600.

Нэгэнт хийсэн QR- задрал, системийн шийдэл Ax=fгурвалжин матрицын системийн шийдэл гэж үзэж болно Р, учир нь учир нь QR=f, Тэр Rx=Q T f:

>> x = R\(Q"*f) x = 1.0000 1.0000 1.0000

Матрицын задралын талаар дэлгэрэнгүй мэдээлэл, харгалзах MATLAB функцууд chol, lu, qr болон тэдгээрийн аргументуудыг Матрицын задрал хэсэгт бичсэн болно.

Шугаман тэгшитгэлийн системийг урвуу налуу зураасаар шийдвэрлэх алгоритм

Шугаман алгебрийн тэгшитгэлийн системийг MATLAB дээр урвуу ташуу зураасаар шийдвэрлэхдээ
x = A\b
алгоритм нь матрицын төрлөөс хамааран LAPACK эсвэл UMFPACK багцын аль нэгэнд хэрэгжсэн хамгийн тохиромжтой аргыг ашиглан системийг шийддэг. Энд b нь мөн матриц байж болох ба мөрийн тоо нь А матрицын мөрийн тоотой давхцаж байна. Дараа нь х матрицыг буцаана, i-р багана бүр нь Ax (i) = b (i) системийн шийдийг агуулна. ) , i=1,2,... ,k, энд b (i) нь b = [ b (1) матрицын i-р багана | b (2) ...| b(k)].

\ үйлдэлд хэрэгжүүлсэн алгоритм нь дараах алхмуудаас бүрдэнэ.

• 1. Өчүүхэн тохиолдолд хэрэв А нь сийрэг, диагональ байвал (Сийрэг матрицууд MATLAB-д сийрэг матрицуудад зориулагдсан) шийдийг энгийн x k = b k /a kk томъёогоор олно, энд k=1,2,. ..н.

2. Хэрэв А нь дөрвөлжин, сийрэг, туузан матриц бол зурвасын матриц шийдэгчийг ашиглана. Хоёр сонголт байж болно:

а. Хэрэв А нь гурвалсан матриц, b нь бодит тоонуудын нэг багана бол системийг Гауссын арилгах замаар шийднэ (түүний үйлдлийг зөвхөн диагональ дээрх элементүүд дээр гүйцэтгэдэг). Хэрэв арилгах явцад тогтвортой байдлыг хадгалахын тулд эгнээний сэлгэлт хийх шаардлагатай бол эсвэл А матриц гурвалсан биш бол дараах цэг ажиллана.
б. Хэрэв А нь параметрээс их тэгээс ялгаатай элементийн нягттай соронзон хальс юм bandden, анхдагчаар 0.5-тай тэнцүү эсвэл өмнөх догол мөрийн нөхцөл хангагдаагүй бол A ба b төрлөөс хамаарч ( давхарэсвэл ганц бие) дараах LAPACK номын сангийн процедурыг нэрлэнэ:

A ба b нь жинхэнэ давхар - DGBTRF, DGBTRS процедурууд
A ба b цогцолбор төрлийн давхар - ZGBTRF, ZGBTRS процедурууд
A эсвэл b бодит төрлийн дан - журам SGBTRF, SGBTRS
A эсвэл b цогц төрлийн дан - CGBTRF, CGBTRS процедур

Тэг биш элементүүдийн нягтыг соронзон хальсны тэгээс бусад элементүүдийн тоог матрицын соронзон хальсны бүх элементүүдийн тоонд харьцуулсан харьцаа гэж ойлгодог, жишээлбэл, загвар нь өгөгдсөн 7-оос 7 хэмжээтэй матрицын хувьд. доор, тэгээс бусад элементийн тоо

nz = 1 (диаграмм No-2 дээр) + 6 (диаграмм No-1 дээр) + 7 (диаграм No0 дээр) + 6 (диаграмм No1 дээр) + 1 (диаграмм No2 дээр) + 1 (диаграмм No3 дээр) = 22,

болон соронзон хальсны бүх элементүүдийн тоо

хамтлаг = 5 (диаграмм No-2 дээр) + 6 (диаграмм No-1 дээр) + 7 (диаграм No0 дээр) + 6 (диаграмм No1 дээр) + 5 (диаграмм No2 дээр) + 4 (диаграмм No3 дээр) = 33

тэгээс бусад элементүүдийн нягт нь 2/3 байх болно. 2/3 > 0.5 тул туузан матрицын уусгагчийг ашиглана
Параметр bandden, MATLAB дахь сийрэг матрицын алгоритмуудыг хянадаг бусад параметрүүдийн нэгэн адил spparms функцийг ашиглан тохируулдаг.



Алгоритмын энэ алхамын утга нь соронзон хальсны матрицтай системийг шийдвэрлэхэд соронзон хальснаас гадуурх үйлдэл хийх шаардлагагүй юм. Хэрэв тэжээл хангалттай дүүрсэн бол тэг элементтэй олон үйлдэл хийхгүй. Эсрэгээр, хэрэв соронзон хальс нь нэлээд сийрэг бол алгоритмын цаашдын алхамуудад өгөгдсөн арга барил нь илүү үр дүнтэй байх болно.

• 3. Хэрэв А нь дээд ба доод гурвалжин матриц бол урвуу орлуулалтын арга буюу үүний дагуу хамгийн сүүлийн (эсвэл эхний тэгшитгэл)-ээс уусмалын бүрэлдэхүүнийг олж, дараа нь олсон бүрэлдэхүүн хэсгүүдийг шууд орлуулах аргыг хэрэглэнэ. Дараахь тэгшитгэлд орлуулж тэгшитгэлийн дараагийн шийдийн бүрэлдэхүүн хэсгүүдийг олно.
• 4. Хэрэв А - сэлгэлтээр гурвалжин хэлбэрт оруулах боломжтой бол харгалзах бууралтыг хийж, дараа нь 3-р алхамын адил тэгшитгэлийн системийг шийднэ.

5. Хэрэв А нь тэгш хэмтэй матриц (эсвэл нийлмэл тохиолдолд Гермит) бөгөөд түүний диагональ нь зөвхөн эерэг бодит элементүүдийг агуулж байвал А нь сийрэг эсэхээс хамаарч a) эсвэл b) зүйл биелнэ.

а. Хэрэв A нь сийрэг биш бол Cholesky задралыг A = R T R, дараа нь R T ба R гурвалжин матрицтай системийг шийдэх оролдлого хийнэ: R T y = b ба Rx = y. Энэ тохиолдолд LAPACK номын сангийн дараах процедурыг нэрлэнэ.

A ба b нь бодит бөгөөд давхар - DLANGE, DPOTRF, DPOTRS, DPOCON
A ба b нь нарийн төвөгтэй бөгөөд давхар - ZLANGE, ZPOTRF, ZPOTRS, ZPOCON
A ба b нь бодит бөгөөд дан төрлийн - SLANGE, SPOTRF, SPOTRS, SDPOCON
A ба b цогцолбор ба нэг төрлийн - CLANGE, CPOTRF, CPOTRS, CPOCON

Хэрэв матриц эерэг тодорхойгүй бол Cholesky задрал амжилтгүй болно. Гэхдээ эерэг тодорхой байдлын урьдчилсан шалгалт байдаггүй бөгөөд энэ нь задралын явцад тодорхойлогддог, учир нь матриц эерэг тодорхой биш гэдгийг тодруулахын тулд Cholesky задралын хэд хэдэн алхамыг хийхэд хангалттай байдаг. Тооцооллын явцад сөрөг тооны квадрат язгуурыг гаргаж авах шаардлагатай болно). Хэрэв Cholesky задрал хангагдаагүй бол дараагийн цэг рүү шилжинэ.

б. Хэрэв A нь сийрэг бол мөр, баганын тэгш хэмтэй сэлгэлтийг эхлээд Чолескийн задралын хүчин зүйлийн дүүргэлтийг багасгахын тулд тэгш хэмийн хамгийн бага зэрэглэлийн алгоритм (функц symmmd) ашиглан гүйцэтгэнэ. дүүргэх явцад үүссэн шинэ 0 биш элементүүдийн тоог багасгахын тулд:

p = symmmd(A) - вектор p нь сэлгэлтийг агуулна

R = chol(A(p, p));

Холескийн үржүүлэгчтэй хоёр системийг шийдсэн бөгөөд эхнийх нь шилжүүлсэн үржүүлэгч ба баруун талын вектор дахь харгалзах сэлгэлттэй.

хоёр дахь нь тэлэлтийн коэффициенттэй бөгөөд шийдлийн бүрэлдэхүүн хэсгүүдийг в векторын харгалзах байрлалд оруулах замаар х
x(p, :) = R\y

• 6. Хэрэв А нь Гессенбергийн матриц бол дээд гурвалжин матриц (баруун талын харгалзах өөрчлөлттэй) болж буураад системийг орлуулалтаар шийднэ.

7. Хэрэв А нь 1-6-р зүйлийн нөхцлийг хангаагүй квадрат матриц бол сийрэг эсэхээс хамаарч дараах үйлдлийг гүйцэтгэнэ.

а. Хэрэв А нь сийрэг матриц биш бол тэргүүлэх элементийг сонгох замаар Гауссын устгах аргыг ашиглан (задралын тогтвортой байдлыг хангах) A = LU матрицын LU задралыг хийнэ.

U - дээд гурвалжин матриц
L нь эгнээний сэлгэн залгалтаар гурвалжин болгон бууруулсан матриц юм

ба Ax = b системийн шийдийг Ly = b, Ux = y гурвалжин матрицтай системүүдийг дараалан шийдвэрлэх замаар олно.
LU задралыг хийхийн тулд LAPACK номын сангийн дараах процедурыг нэрлэнэ.

A ба b нь бодит ба давхар - DLANGE, DGESV, DGECON
A ба b нь нарийн төвөгтэй бөгөөд давхар - ZLANGE, ZGESV, ZGECON
A ба b нь бодит бөгөөд дан төрлийн - SLANGE, SGESV, SGECON
A ба b нь нарийн төвөгтэй бөгөөд нэг төрлийн - CLANGE, CGESV, CGECON

б. Хэрэв А нь сийрэг матриц бол задралыг олох явцад L ба U хүчин зүйлийн дүүргэлтийг багасгахын тулд багануудыг дахин байрлуулна. Цаашилбал, LU задралын явцад мөрүүдийг дахин цэгцлэх замаар тооцооллын тогтвортой байдлыг хангаж, дараа нь гурвалжин матрицтай системийг дахин шийддэг. Сийрэг матрицын LU задралыг хийхийн тулд UMFPACK номын сангийн процедурыг ашигладаг.

8. Хэрэв алгоритмын өмнөх цэгүүд ажиллахгүй байсан тул А нь квадрат матриц биш бол бүх зүйл түүний сийрэг байдлаар тодорхойлогддог бөгөөд доорх цэгүүдийн аль нэг нь ажиллана.

а. Хэрэв А нь сийрэг матриц биш бол QR задрал AP = QR хийгдэх ба P нь баганын сэлгэцийн матриц, Q нь ортогональ матриц (Q T Q = I), R нь дээд гурвалжин юм. Хэрэв A нь m-ээр n хэмжээтэй бол Q нь m-ээр, R нь m-ээр n хэмжээтэй байна. Дараа нь системийн шийдлийг дараах байдлаар олно.

x = P*(R \ (Q" * b))

Ax = b ба AP = QR-аас хойш дараах байдалтай байна: QRx = bP ба Rx = Q T bP.

б. А сийрэг ба тэгш өнцөгт матрицын хувьд Q матрицыг тооцоолох нь утгагүй, учир нь энэ нь бөглөгдөх магадлалтай. Тиймээс QR задралын алгоритм нь c = Q T b (өөрөөр хэлбэл өөрчлөгдсөн баруун гар тал) -ийг тооцоолж, Rx = c системийг гурвалжин матрицаар шийдэж анхны Ax = b системийн шийдлийг гаргана.

Дээрх бүх зүйлээс гадна дээрх алгоритм нь матрицын нөхцөл байдлыг үнэлж, матриц муу нөхцөлдсөн тохиолдолд шийдэлд гарч болзошгүй алдааны тухай анхааруулгыг харуулна (Матрицын нөхцөл байдлын нарийвчлалд үзүүлэх нөлөөллийг үзнэ үү. түүнтэй систем шийдвэрлэх). Дээрх алгоритм нь нэмэлт цаг хугацаа шаардагдах янз бүрийн шалгалтуудыг агуулдаг. Дараагийн хэсэг болох Шугаман тэгшитгэлийн системийг шийдвэрлэх linsolve функц нь матрицын төрлийг зааж өгөх боломжийг олгодог бөгөөд ингэснээр тооцоолох хугацааг багасгадаг.

Шугаман тэгшитгэлийн системийг шийдвэрлэх linsolve функц

Шугаман алгебрийн тэгшитгэлийн системийг (эсвэл матрицад тодорхойлогдсон олон баруун талтай системүүд) урвуу зураасаар шийдэхийн оронд linsolve функцийг ашиглаж болох бөгөөд энэ нь \ үйлдлийн алгоритмд хамаарах бүх матрицын шалгалтыг хийдэггүй. өмнөх хэсгийг үзнэ үү).

Linsolve функц нь хоёр оролт, нэг гаралтын аргумент бүхий хамгийн энгийн хэлбэрээр дуудагдсан
x = linsolve(A, b)
матриц квадрат эсэхээс хамаарч Ax = b системийг аль нэг аргаар шийддэг.

• Хэрэв А нь квадрат матриц бол эхлээд түүний LU задралыг тооцоод дараа нь L ба U гурвалжин матрицтай хоёр системийг шийднэ.
• Хэрэв А нь тэгш өнцөгт матриц бол эхлээд түүний QR задралыг тооцоод дараа нь гурвалжин матрицтай системийг шийднэ.

(Үргэлжлүүлэн өргөтгөх хүчин зүйл бүхий үйлдлүүдийн талаарх дэлгэрэнгүй мэдээллийг энэ хэсэгт бичсэн болно). Түүнчлэн, хэрэв А матриц муу нөхцөлтэй эсвэл А нь бүрэн бус зэрэглэлийн матриц бол холбогдох анхааруулга гарч ирнэ, жишээлбэл:

A = ; b = ; x = linsolve(A,b) Анхааруулга: Зэрэглэл дутмаг, зэрэглэл = 1, tol = 4.4686e-015. x = 0 0 2.0000

Энэ мессежийг командын цонхонд хэвлэхээс урьдчилан сэргийлэхийн тулд linsolve функцийг хоёр гаралтын аргументаар дуудна уу.
= linsolve(A, b)
Үүний үр дүнд гарсан шийдлийг х, r дээр бичнэ - матрицын зэрэглэл (хэрэв А нь тэгш өнцөгт матриц бол), эсвэл түүний нөхцлийн дугаарын тооцооны эсрэг (хэсгийг үзнэ үү), жишээ нь.

A = ; b = ; = linsolve(A,b) x = -1.0000e+000 9.9999e-001 3.3307e-006 r = 6.9444e-013

Тэгшитгэлийн системийн матрицын төрлийг зааж өгөх үед linsolve функцийн гол давуу тал нь \ үйлдлээр илэрдэг. Үүнийг хийхийн тулд linsolve функцийг дуудахын өмнө та дараах талбарууд бүхий матрицын талаарх мэдээллийг агуулсан бүтцийг бөглөх хэрэгтэй.

• SYM - тэгш хэмтэй;
• LT - доод гурвалжин;
• UT - дээд гурвалжин;
• UHESS - Хессенберг;
• POSDEF - тэгш хэмтэй, эерэг тодорхой;
• RECT - тэгш өнцөгт;
• TRANSA - өгөгдсөн матрицтай системийг шийдвэрлэх шаардлагатай эсэх.

Талбар бүр үнэн эсвэл худал байж болно. Мэдээжийн хэрэг талбарын утгуудын бүх хослолууд хүчинтэй биш, жишээлбэл, матриц нь гурвалжин хэлбэртэй байж болохгүй, нэгэн зэрэг тэгш хэмтэй, эерэг тодорхойлогддог. Талбайн утгуудын зөв хослолыг дараах хүснэгтэд цуглуулав

LT	UT	UHESS	SYM	POSDEF	RECT	ТРАНСА
үнэн	худлаа	худлаа	худлаа	худлаа	Үнэн худал	Үнэн худал
худлаа	үнэн	худлаа	худлаа	худлаа	Үнэн худал	Үнэн худал
худлаа	худлаа	үнэн	худлаа	худлаа	худлаа	Үнэн худал
худлаа	худлаа	худлаа	үнэн	үнэн	худлаа	Үнэн худал
худлаа	худлаа	худлаа	худлаа	худлаа	Үнэн худал	Үнэн худал

Хэрэв системийн матриц эерэг тодорхой бол түүнийг шийдвэрлэхдээ үүнийг анхаарч үзэх хэрэгтэй, учир нь эерэг тодорхой матрицуудын хувьд шийдэл нь ерөнхий квадрат матрицтай системийг шийдвэрлэхэд ашигладаг LU задралаас цөөн үйлдэл шаарддаг Чолескийн задралд суурилдаг. . Дараах жишээний тусламжтайгаар үүнийг шалгахад хялбар бөгөөд үүнд тэгш хэмтэй эерэг тодорхой матриц (санамсаргүй тоонуудын матрицыг шилжүүлэн суулгаж, диагональ дээр их тоонуудыг нэмж оруулсан) болон системийн Энэ матрицтай тэгшитгэлийг эхлээд ерөнхий хэлбэрийн матрицтай систем (opts. SYM = худал ба opts. POSDEF = худал), дараа нь тэгш хэмтэй ба эерэг тодорхой матрицтай (opts.SYM = үнэн ба opts) гэж шийддэг. .POSDEF = үнэн).

% SYM болон POSDEF opts-аас бусад ops бүтцийн бүх талбарыг тохируулна. TRANSA = худал; opts.UHESS = худал; opts.RECT ​​= худал; opts.UT = худал; opts.LT = худал; % N = 2 хэмжээтэй матрицын вектор үүсгэх.^(8:12); % шийдлийн хугацааг бичихийн тулд хоосон массив үүсгэх TimeGeneral = ; TimePosSym =; % гогцоонд бид матрицуудыг үүсгэж, n = N -ийн шийдлийн хугацааг харьцуулна % тэгш хэмтэй эерэг тодорхой матриц % ба баруун талын вектор A = rand(n); A = A + A" + 2*n*eye(n); b = нийлбэр(A, 2); % системийг ерөнхий матрицтай системээр шийднэ opts.SYM = худал; opts.POSDEF = худал; Tstart = cputime; x = linsolve(A,b, opts); Tend = cputime; TimeGeneral =; % системийг тэгш хэмтэй ба байрлалын матрицтай систем гэж шийднэ opts.SYM = үнэн; opts.POSDEF = үнэн; Tstart = cputime; x = linsolve( A,b, opts); Tend = cputime; TimePosSym = ; төгсгөл % харуулах цагийн график дүрс логлог(N, TimeGeneral, N, TimePosSym) тайлбар("TimeGeneral", "TimePosSym")

Системийг шийдвэрлэх эдгээр аргуудын үр дүнд гарсан тооцооллын зардлыг доорх графикт үзүүлэв

Мэдээжийн хэрэг, хэрэв матриц нь гурвалжин бол гурвалжин матрицтай системийг шийдэх нь O(n 2) үйлдлээр хийгддэг тул үүнийг зааж өгөх нь маш чухал бөгөөд хэрэв матрицад зориулагдсан шийдлийн алгоритм нь матрицад зориулагдсан бол. гурвалжин матрицтай системд ерөнхий хэлбэрийг хэрэглэвэл ойролцоогоор O(n3) үйлдлийг хийх болно.

Linsolve функц нь матриц нь заасан шинж чанаруудыг хангаж байгаа эсэхийг шалгадаггүй бөгөөд энэ нь алдаа гаргаж болзошгүй юм. Жишээ нь, хэрэв, дараах матрицтай системийг шийдвэрлэхдээ баруун гар талтай

A = ; b = ; UT талбарт үнэнийг тохируулах (бусад бүх зүйлийг худал болгох) opts.UT = үнэн; opts.TRANSA = худал; opts.LT = худал; opts.UHESS = худал; opts.SYM = худал; opts.POSDEF = худал; opts.RECT ​​= худал; дараа нь системийг шийдэхдээ linsolve функц нь матрицыг дээд гурвалжин гэж үзэж, дээд гурвалжнаас өөрт хэрэгтэй элементүүдийг сонгоно A x = linsolve(A,b, opts) Үүний үр дүнд x = 1 1 1 шийд гарна. матрицад харгалзах A = ;

Матрицын нөхцөл байдлын нөлөөлөл нь системийг шийдвэрлэх нарийвчлалд нөлөөлдөг

Энэ хэсэгт бид баруун талын векторын элементүүд болон Ax = b шугаман тэгшитгэлийн системийн матриц дахь алдаа нь тухайн системийн шийдэлд хэрхэн нөлөөлж болохыг харна. Эхлээд баруун талын векторт эвдрэл оруулах тохиолдлыг авч үзье b. Тиймээс бид хоёр системийг шийддэг

Түүгээр ч зогсохгүй бид систем бүрийг яг таг шийддэг гэж үзэж байгаа бөгөөд (1) системийн x шийдэл нь баруун талдаа δb гажигтай (2) системийн шийдлээс хэр ялгаатай байх вэ гэсэн гол асуулт гарч ирж байна. Зарим хэмжилтийн үр дүнд баруун талд байгаа элементүүдийг b k бүрэлдэхүүн хэсэг бүрт δb k алдаа агуулсан байх тул энэ нь нэлээд чухал асуулт юм. Ижил хэмжигдэхүүнийг хэмжихэд (тус бүр өөрийн гэсэн жижиг алдаатай) баруун талдаа арай өөр системүүдийн тохирох шийдлүүд нь бие биенээсээ тийм ч их ялгаатай байдаггүйг би хүсч байна. Харамсалтай нь энэ нь үргэлж тийм байдаггүй. Үүний шалтгаан нь түүний гэж нэрлэгддэг матрицын шинж чанар юм нөхцөл байдал. Энэ талаар цаашид хэлэлцэх болно.

Эхлээд та вектор ба x-ийн ойролцоо хэмжүүрийг нэвтрүүлэх хэрэгтэй, i.e. алдааны вектор. Векторын хэмжээг хэмжих хэмжүүр нь норм юм (үүнийг янз бүрийн аргаар тодорхойлж болно). Одоохондоо векторын ердийн Евклидийн нормыг (түүний бүрэлдэхүүн хэсгүүдийн квадратуудын нийлбэрийн квадрат язгуур) норм болгон авч үзье.

Үүний дагуу

Энд n нь систем дэх үл мэдэгдэх болон тэгшитгэлийн тоо юм. Векторын хэмжээг тооцоолохын тулд векторын нормоос гадна матрицын хэмжээг тооцоолох матрицын норм хэрэгтэй. Дараах байдлаар тодорхойлогдсон матрицын нормыг авч үзье (үүнийг спектрийн норм гэж нэрлэдэг):

тэдгээр. спектрийн матрицын норм нь матрицын хамгийн их хувийн утгын квадрат язгууртай тэнцүү A T A. MATLAB нь матриц ба векторуудын нормыг тооцоолох норм функцтэй бөгөөд ялангуяа дээрх нормуудыг тооцоолох боломжтой. Яагаад бид вектор ба матрицын эдгээр тодорхой нормуудыг сонгосон бэ гэдгийг хэд хэдэн тооцоолол, тодорхойлолтыг өгсөн хэсэгт дэлгэрэнгүй тайлбарласан болно. Энэ нь системийг шийдвэрлэхэд алдаа гаргахад ашиглах тооцоотой холбоотой (энэ тэгш бус байдлын гарал үүслийг мөн дурдсан хэсэгт өгсөн болно):

Энд бид матрицын нөхцөлийн дугаарыг тэмдэглэж, дараах байдлаар тодорхойлогдоно.

Дээрх тэгш бус байдлаас үзэхэд системийн матрицын нөхцөлийн тоо их байх тусам шийдэл дэх харьцангуй алдаа нь баруун талын жижиг алдаатай байж болно.

Нөхцөл байдал муутай матрицын сонгодог жишээ болох Гильберт матрицыг авч үзээд системийн баруун талд байгаа алдаа нь шийдлийн алдаанд хэрхэн нөлөөлж байгааг олж мэдье. Хилбертийн матрицыг дараах байдлаар тодорхойлно

Hilbert матрицыг үүсгэхийн тулд MATLAB нь hilb функцийг өгдөг бөгөөд түүний оролтын аргумент нь матрицын хэмжээг тодорхойлдог. 6-аас 6 хэмжээтэй жижиг матрицыг авъя:

N = 6; H = hilb(n) H = 1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 300.306. 0.1429 0.1250 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.2000 0.1667 0.1429 0.1250 0.1111 0.10102 0.10102. 111 0.1000 0.0909

X = нэг (n, 1); b = H*x b = 2.4500 1.5929 1.2179 0.9956 0.8456 0.7365

Баруун талд байгаа матриц эсвэл векторын аль алинд нь "сэжигтэй" зүйл байхгүй гэдгийг бид харж байна; бүх тоонууд бие биенээсээ тийм ч их ялгаатай биш юм. Одоо b вектор дээр 10 -5 гэсэн дарааллаар бага тоонуудыг нэмж, цочирдсон баруун талын b + δb-г үүсгэж, цочирдсон баруун талтай системийг шийдэж векторыг гаргая.

Delta_b = 1e-5*(1:n)"; x_tilda = H\(b + delta_b) x_tilda = 0.9978 1.0735 0.4288 2.6632 -1.0160 1.8593

Үүссэн шийдэл нь бүх нэгж байх ёстой яг нэгээс хол байгааг харж болно. Уусмалын болон баруун талын харьцангуй алдааг тооцоолъё (норм функц нь анхдагчаар векторын Евклидийн нормыг тооцдог):

Delta_x = x - x_tilda; ЗҮҮН = норм(дельта_х)/норм(х) ЗҮҮН = 1.1475 БАРУУН = норм(гурвалжин_б)/норм(б) БАРУУН = 2.7231e-005

Тиймээс, шийдэл дэх алдаа нь нэгдмэл байдлын дарааллаар байна, гэхдээ баруун талын өөрчлөлтүүд нь 10 -5 дарааллаар байсан. Энэ нь дээрх алдааны тэгш бус байдалд бүрэн нийцдэг. Үнэн хэрэгтээ, cond гэж нэрлэгддэг MATLAB функцийг ашиглан cond(H) нөхцлийн тоог тооцоод үзье. матрицын спектрийн нормын хувьд

C = cond(H) c = 1.4951e+007

ЗҮҮН ≈ 1.1475 бага

C* ЗӨВ ҮҮ? 1.4951e+07 * 2.7231e-05 ≈ 407

тэгш бус байдал хангагдсан (зарим маржинтай ч гэсэн).

Хилберт матрицын хэмжээ ихсэх тусам шийдлийн алдаа зөвхөн нэмэгдэх болно (үүнийг n = 7, 8, ... гэж тохируулснаар шалгахад хялбар). Үүнээс гадна, n = 12-ийн хувьд матрицын нөхцөл муу, шийдэл буруу байж магадгүй гэсэн мессеж гарч ирнэ.

Анхааруулга: Матриц нь дан хэмжээтэй ойрхон эсвэл муу масштабтай байна.
Үр дүн буруу байж магадгүй. RCOND = 2.409320e-017.

Нөхцөл байдлын хэмжүүрийн хувьд энд сонгогдсон утга нь RCOND нь нөхцөлийн дугаарын тооцоонд хуваагдсантай тэнцүү байна (нөхцлийн дугаарыг тусламжид илүү дэлгэрэнгүй тайлбарласан cond-аас хамаагүй хурдан ажилладаг нэлээн хурдан алгоритм ашиглан тооцоолсон болно. rcond функц дээр). Хэрэв RCOND-ийн утга бага байвал матрицыг нөхцөл муутай гэж үзнэ.

Гилберт матрицын хэмжээ ихсэх тусам шийдлийн алдаа ихсэх нь Гильберт матрицын нөхцөлийн тоо хэмжээ нь маш хурдан өсдөгтэй холбоотой юм. Энгийн гогцоо болон семилогийн функцийг ашиглан үүнийг шалгахад хялбар байдаг (ординатын тэнхлэгийн дагуух масштаб нь логарифм юм):

N = 1:20; C = тэг (1, 20); хувьд n = N H = hilb(n); C(n) = cond(H); төгсгөлийн семилоги(N, C) сүлжээ асаалттай, гарчиг("cond(H)"), xlabel("n")

Дашрамд хэлэхэд, cond функц нь нөхцөлийн дугаарыг тоон аргаар олдог тул (тухайлбал, ганц тоонуудыг олох цорын ганц өргөтгөл) n = 12-оос хойшхи нөхцөлийн дугаарыг зөв тооцоолохоо больсон; үнэн хэрэгтээ энэ нь цаашид өсөх ёстой. MATLAB дахь симбол тооцоолол, өгөгдсөн тооны чухал тоонуудтай үйлдлүүдийг ашиглан баталгаажуулна

N = 1:20; C = тэг (1, N); цифр(60) n = N H = vpa(sym(hilb(n))); Хилбертийн матрицын % тооцоо 60-р оронтой сигма = svd(H); % Хилберт матрицын ганц утгыг олох % Хилберт матрицын нөхцөлийн дугаарыг тооцоолох C(n) = max(давхар(сигма))/мин(давхар(сигма)); төгсгөлийн семилоги(N, C) сүлжээ асаалттай, гарчиг("cond(H)"), xlabel("n")

Одоо энэ жишээтэй холбоотой гурван чухал зүйлийг авч үзье.

Тэдний эхнийх нь Hx = b системийг (нэгжийн шийдэлд харгалзах баруун талын вектортой) буцааж ташуу зураастай оператор ашиглан яг нэгжийг өгөхгүй, алдаа нь аль хэдийн арав дахь оронтой байх болно (хэдийгээр MATLAB-д бүгдээрээ). Тооцоолол нь анхдагчаар давхар нарийвчлалтайгаар хийгддэг)

Format long H\b ans = 0.99999999999916 1.00000000002391 0.99999999983793 1.00000000042209 0.999999999533060 10800

Энэ нь H матрицыг бүх нэгийн вектороор үржүүлэх үед b векторыг тооцоолохдоо алдаа гарсан тул ийм зүйл тохиолддог. Нэмж дурдахад, системийг шийдвэрлэх явцад дугуйрсан алдаанууд мөн үүрэг гүйцэтгэсэн бөгөөд матрицын нөхцөл байдал муу (жижиг хэмжээтэй ч гэсэн) нь шийдэлд ийм алдаа гаргахад хүргэсэн. Үнэн хэрэгтээ нөхцөл байдлын тоо багатай жижиг матрицуудын хувьд ийм нөлөө ажиглагдахгүй. Санамсаргүй тоонуудын 6-аас 6 матрицыг авч, нөхцөлийн тоог тооцоолъё

A = ранд(n); cond(A) ans = 57.35245279907571

Дараа нь бид бүх нэгжийн яг шийдэлд тохирсон баруун гар талыг бүрдүүлнэ

X = нэг (n, 1); b = A*x;

болон системийг шийдэж, үр дүнд нь сайн нарийвчлалтай болно

>> A\b ans = 1.00000000000000 1.000000000000000 1.000000000000000 1.0000000000000000 1.00000000000000000000000000001

Хоёр дахь чухал цэг нь матрицын тодорхойлогчтой холбоотой юм. Системийг шийдсэн 6-6 Гильберт матрицын тодорхойлогчийг тооцоолъё.

>> det(hilb(6)) ans = 5.3673e-018

Тодорхойлогч нь хангалттай жижиг болж хувирсан бөгөөд үүнээс үүдэн системийн баруун талд бага зэрэг гажигтай шийдэлд гарсан том алдааны асуудлын эх үүсвэр нь тодорхойлогчийн жижиг байдал юм гэсэн буруу дүгнэлт хийж болно. Бодит байдал дээр энэ нь тийм биш бөгөөд хэрэв системийн тодорхойлогч бага бол энэ нь матриц муу нөхцөлтэй гэсэн үг биш бөгөөд иймээс шийдэлд том алдаа байна. Үнэндээ матрицыг авч үзье

A = ;

Түүний тодорхойлогч нь маш бага, ойролцоогоор 10 -121 байна

Det(A) ans = 9.9970e-121

("маш" гэдэг үг нь мэдээжийн хэрэг нөхцөлтэй, гэхдээ энэ нь системийг шийдвэрлэхэд асуудалтай тулгарсан 6-аас 6 хүртэлх Гильберт матрицын тодорхойлогчоос бага юм). Гэсэн хэдий ч тодорхойлогчийн жижиг байдал нь системийн баруун тал эвдэрсэн үед шийдлийн алдаанд ямар ч байдлаар нөлөөлөхгүй бөгөөд энэ нь мэдэгдэж буй шийдэл бүхий системийг бий болгох, баруун талд эвдрэлийг оруулах, шийдвэрлэхэд хялбар байдаг. систем:

X = ; b = A*x; delta_b = 1e-5*; x_tilda = A\(b+delta_b); delta_x = x - x_tilda; ЗҮҮН = норм(гурвалжин_х)/норм(х) БАРУУН = норм(дельта_б)/норм(б) ЗҮҮН = 2.1272e-005 БАРУУН = 2.1179e-005

Тэгэхээр дээрх А матрицын нөхцөлийн дугаар 1-ээс арай их байх тул шийдэл дэх харьцангуй алдаа нь баруун талын харьцангуй алдаатай бараг тэнцүү байна, тухайлбал:

C = cond(A) c = 1.0303

Эцэст нь, шийдлийн алдааны хувьд тэгш бус байдалд тэнцүү тэмдэгт хүрэхтэй холбоотой гурав дахь асуултыг авч үзье.

Өөрөөр хэлбэл, бид олж мэдье: системийн баруун талд бага зэрэг харьцангуй цочрол үүсгэх нөхцөл байдал байж болох уу, 10-5 гэж хэлье, системийн матрицын нөхцөлийн тоо 10 10-тай тэнцүү байна. , мөн уусмалд 10 5-ын харьцангуй алдаа гарна. Та олон жишээг үзэж, янз бүрийн матрицуудыг туршиж үзээд тэгш байдалд хүрч чадахгүй бөгөөд энэ нь шийдлийн алдааны хувьд дээрээс хэтрүүлсэн үнэлгээ гэж буруу дүгнэж болно. Гэсэн хэдий ч энэ нь тийм биш бөгөөд дараах жишээ бидэнд итгүүлж байна.

баруун талын харьцангуй цочрол нь 10 -5 байна

БАРУУН = норм(дельта_б)/норм(б) БАРУУН = 1.0000e-005

Системийг шийдвэрлэхэд харьцангуй алдаа 10 5 болж хувирна

X = A\b; x_tilda = A\(b+delta_b); delta_x = x - x_tilda; ЗҮҮН = норм(дельта_х)/норм(x) ЗҮҮН = 1.0000e+005

Мөн энэ нь яагаад тохиолддог
1) энэ жишээнд А матрицын нөхцөлийн дугаар 10 10;

C = cond(A) c = 1.0000e+010

2) шийдлийн алдааны тэгш бус байдал нь тэгш байдал болж хувирна.

Хэрэв бид урт форматыг тохируулсан бол ЗҮҮН, БАРУУН болон нөхцөлийн дугаар нь яг 10 5 , 10 -5 ба 10 10 биш байгааг харж болно, гэхдээ энэ нь дугуйрсан алдаатай холбоотой юм. Хэрэв яг арифметик аргаар шийдсэн бол тэгш байдал яг тодорхой байх бөгөөд үүнийг аналитик байдлаар харуулах боломжтой (хэсгийг үзнэ үү).

Өмнөх жишээнүүдэд бид матриц нь алдаа агуулаагүй бөгөөд алдаа нь зөвхөн шугаман тэгшитгэлийн системийн баруун талд байж болно гэж үзсэн. Практикт системийн матрицын элементүүдийг алдаатай зааж өгсөн байдаг, жишээлбэл. системийн оронд

|| Сүх || V = || б || V ⇒ || A || М || x || V ≥ || б || В

хаана || || M нь зарим матрицын норм юм. Үүнийг хийхийн тулд матрицын норм || || M ба векторын норм || || V нь дараах тэгш бус байдлыг хангах ёстой

|| A || М || x || V ≥ || Сүх || В

дурын матрицууд ба х векторуудын хувьд. Хэрэв энэ тэгш бус байдал хангагдвал матрицын норм || || М гэж нэрлэдэг тохиролцсонвектор нормтой || || В. Жишээлбэл, спектрийн нормыг мэддэг

(A T матрицын хамгийн их хувийн утгын квадрат язгуур) нь Евклидийн векторын нормтой нийцэж байна

Тийм ч учраас энэ хэсэгт бид эдгээр нормыг ашиглан бүх туршилтыг хийсэн.

Тэгш бус байдлыг хүлээн авснаар || A || М || x || V ≥ || б || V цаашид тэмдэглэхэд Ax = b-ээс дараах нь . А матриц нь ганц бие биш тул δx = A -1 δb ба || δx || V = || A -1 δb || В. Дахин бид нормын тууштай байдлыг ашиглаж, || тэгш бус байдлыг олж авна δx || V ≤ || A -1 || М || δb || В. Цаашилбал, олж авсан хоёр тэгш бус байдалд

|| A || М || x || V ≥ || б || V ба || δx || V ≤ || A -1 || М || δb || В

Бид нэг тэгш бус байдлын бага утгыг нөгөө тэгш бус байдлын том утгад, том утгыг тус тус бага болгон хуваана.

энгийн хувиргалтаар бид эцэст нь шаардлагатай тэгш бус байдлыг олж авдаг

Cond(A) = || A || М* || A -1 || М.

Алдааны тэгш бус байдлыг гаргахдаа бид зөвхөн матрицын норм нь векторын нормтой нийцэж байгааг л ашигласан гэдгийг анхаарна уу. Энэ нь зөвхөн матрицын спектрийн норм, векторын Евклидийн норм төдийгүй бусад нормуудын хувьд ч үнэн юм. Тиймээс, жишээ нь, хамгийн их баганын матрицын нормыг томъёогоор тооцоолно

Эхний векторын нормтой нийцэж байна

ба томьёогоор тооцсон эгнээний матрицын дээд норм

хязгааргүй вектор нормтой нийцэж байна

Норм функц нь зөвхөн векторын Евклидийн норм, матрицын спектрийн нормыг тооцдог төдийгүй дээр дурдсан вектор ба матрицын нормуудыг тооцдог. Үүнийг хийхийн тулд та үүнийг нэмэлт хоёр дахь аргументаар дуудах хэрэгтэй.

• q = норм(А, 1) - А матрицын баганын дээд норм
• q = норм(A, inf) - А матрицын мөрийн дээд норм
• q = норм(a, 1) - a-ийн эхний вектор норм
• q = норм(a, inf) - хязгааргүй вектор норм a

Матрицын нөхцөлийн дугаар cond(A) = || A || М* || A -1 || Төрөл бүрийн матрицын нормуудын хувьд M-ийг cond функцийг ашиглан тооцоолж болно. Хэрэв cond-ийг нэг оролтын аргументаар (матриц) дуудсан бол нөхцөлийн дугаарыг спектрийн матрицын нормтой харьцуулан тооцно. Cond функцийг нэмэлт аргументаар дуудах нь тогтоосон матрицын нормтой харьцуулахад нөхцөлийн дугаарыг буцаана:

• c = cond(A, 1) - матрицын хамгийн их баганын нормтой харьцуулахад нөхцөлийн дугаар
• с = cond(A, inf) - матрицын мөрийн дээд нормтой харьцуулахад нөхцөлийн дугаар

Алдааны тэгш бус байдалд матрицын норм векторын нормтой нийцэж байх нь чухал болохыг харуулсан жишээ болгон А матриц, баруун талын b вектор, баруун талын delta_b алдааны вектортой жишээг үзүүлэв.

A = ; b = [ -5.7373057243726833e-001 -1.5400413072907607e-001 -5.3347697688693385e-001 -6.0209490373259589e-00 delta_b = [-0.71685839091451e-5 0.54786619630709e-5 0.37746931527138e-5 0.20850322383081e-5];

Эхний векторын нормыг ашиглан тооцооны баруун ба зүүн хэсгийг, спектрийн матрицын нормтой уялдуулан матрицын нөхцөлийн дугаарыг тооцъё.

БАРУУН = норм(гурвалжин_б,1)/норм(б,1); c = нөхцөл (A); x = A\b; x_tilda = A\(b+delta_b); delta_x = x - x_tilda; ЗҮҮН = норм(дельта_х,1)/норм(x,1); богино e disp формат ()

Бид тэгш бус байдлын зүүн ба баруун талын дараах утгыг олж авна
9.9484e+004 9.9323e+004

Зүүн тал нь баруун талаас хэтрэх ёсгүй (дээр нотлогдсон), гэхдээ үл нийцэх хэм хэмжээг сонгосон тул илүү том болсон.

Одоо матрицын нөхцөлийн тоо яагаад нэгээс бага байж болохгүйг авч үзье. А матрицын нөхцөлийн дугаарыг cond(A) = || гэж тодорхойлно A || М* || A -1 || М , хаана || A || M нь A-ийн зарим матрицын норм юм. Матрицын норм (өөрөөр хэлбэл, тоо нь матриц тус бүртэй холбоотой байх дүрэм) дур зоргоороо байж болохгүй, энэ нь дараах дөрвөн аксиомыг хангасан байх ёстой.

A1. || A || Аливаа матрицын хувьд ≥ 0 ба || A || Зөвхөн А нь тэг матриц бол = 0.

А2. || αA || = | α | * || A || дурын матриц А ба α тооны хувьд.

A3. || A + B || ≤ || A || + || B || А ба В матрицуудын хувьд

А4. || AB || ≤ || A || * || B || ямар ч А ба В матрицын хувьд.

Сүүлчийн аксиомоос харахад нормыг зөвхөн квадрат матрицын хувьд тодорхойлсон нь тодорхой байна (хэдийгээр төрөл бүрийн нормыг тооцоолох дээрх томъёонд зарчмын хувьд ийм хязгаарлалт байхгүй). Нэмж дурдахад, сүүлчийн аксиомоос харахад I матрицын аливаа норм нэгээс багагүй, үнэндээ

|| би || = || I*I || ≤ || би || 2 ⇒ || би || ≥ 1.

Дараа нь дөрөв дэх аксиомыг ашиглан бид матрицын нөхцөлийн дугаар үргэлж нэгээс их байгааг олж мэдэв (дурын матрицын нормтой харьцуулахад матрицын нөхцөлийн дугаарын хувьд үнэн)

1 ≤ || би || = || АА -1 || ≤ || A || * || A -1 || = нөхцөл (А).

Баруун тал нь эвдэрсэн үед шийдлийн алдааг тооцоолоход яг тэгш байдал үүссэн шалтгааныг судалж, энэ хэсгийг дуусгая.

мөн MATLAB дээр харгалзах жишээг бүтээх. (Доорх хэлэлцүүлгийг тухайлбал, Ж. Форсит, К. Молер нарын номонд багтаасан болно. Шугаман алгебрийн тэгшитгэлийн системийн тоон шийдэл. М: "Мир", 1969.)

Матрицын ганцаарчилсан задралын тухай теорем үндэслэл гаргахад чухал үүрэг гүйцэтгэдэг бөгөөд үүний дагуу n хэмжээтэй аливаа бодит матрицын хувьд n-ээр n хэмжээтэй U ба V ортогональ матрицууд байдаг (U T U=UU T ба V T V = VV T) D = U T AV үржвэр нь диагональ матриц байх ба бид U ба V-ийг сонгох боломжтой.

Энд μ 1 ≥ μ 2 ≥…≥μ r ≥ μ r+1 =…=μ n =0,

ба r нь А матрицын зэрэглэл. μ k тоонуудыг А матрицын спектрийн тоо гэнэ. Ганц бус А матрицын хувьд дараах үнэн байна.

μ 1 ≥ μ 2 ≥ … ≥μ n ≥ 0.

Дараагийн чухал баримт бол ортогональ матрицаар үржүүлэх нь векторын Евклидийн нормыг өөрчлөхгүй, өөрөөр хэлбэл. n элементтэй дурын х вектор ба n х n хэмжээтэй U ортогональ матрицын хувьд тэгш байдал үнэн

|| Ux || = || x ||.

Ортогональ матрицаар үржүүлэх нь спектрийн нормыг өөрчлөхгүй тул

Тиймээс матрицын нөхцлийн дугаарын хувьд дараах тэгшитгэл үнэн байна.

Бидэнд хоёр систем бий: Ax = b (яг шийдэлтэй x) ба (яг шийдэлтэй). Мэдээжийн хэрэг, δx алдаа нь баруун тал нь δb цочрол бүхий системийн шийдэл юм, өөрөөр хэлбэл. системүүд Aδx = δb. A матрицын ганц утгын задралыг D = U T AV гэж үзье, дараа нь U ба V нь ортогональ матриц учраас UDV T = A болно. Цаашид

Ax = b ⇒ UDV T x = b.

Тэмдэглэгээг танилцуулъя

x" = V T x, b" = U T b,

Дараах системүүд тэнцүү байна

Ax = b ⇔ Dx" = b"

Үүнтэй ижил төстэй байдлаар системийг алдааны талаар авч үзье

Aδx = δb ⇒ UDV T δx = δb

Бид тэмдэглэгээг танилцуулж байна

δx" = V T δx, δb" = U T δb,

Үүний тулд дараах системүүд тэнцүү байна

Aδx = δb ⇔ Dδx" = δb"

Тэдгээр. Бид диагональ матрицтай энгийн эквивалент системийг олж авсан бөгөөд тэдгээрийн диагональ дээр А матрицын спектрийн тоонууд байрладаг.

Одоо эдгээр системүүдийн баруун талыг тусгай аргаар сонгоцгооё, тухайлбал, let

Энд β > 0 байвал Dx" = b" системийн тохирох шийдэл болно

Энд μ 1 нь А матрицын хамгийн их цорын ганц утга юм. Бид Dδx" = δ b" системтэй ижил зүйлийг хийх болно, тухайлбал, үзье.

Энд γ > 0 бол Dδx" = δb" системийн тохирох шийдэл байх болно.

Векторыг ортогональ матрицаар үржүүлэхэд түүний нормыг хадгалснаас үзэхэд дараах байдалтай байна.

β/μ 1 = || x" || = || V T x || = || x || ба γ/μ n = || δx" || = || V T δx || = ||δx ||.

Яг ижил аргаар бид тэгш байдлыг олж авна:

β = || b" || = || U T b || = || b || ба γ = || δb" || = || U T δb || = || δb ||.

ба түүнээс хойш

тэгээд бид эцэст нь хүрнэ

Тиймээс, А матриц бүрийн хувьд системийн баруун талд, түүний цочролд вектор байгуулах боломжтой бөгөөд ингэснээр шийдэл дэх алдаа нь матрицын нөхцөлийн дугаар ба баруун талын алдааны үржвэр болно. MATLAB дээр харгалзах бүтцийг ганц утгын задралгүйгээр хийж болно (хэдийгээр үүнийг svd функцийг ашиглан олж болно).

Эхлээд бид n-ийг тогтоож, санамсаргүй тооноос n-ээр n матрицын QR задралыг хийснээр U ба V хоёр ортогональ матрицыг олж авна.

N = 4; = qr(ранд(n)); = qr(ранд(n));

D = диаг();

Үүний дараа бид диагональ D матриц ба U ба V ортогональ матрицуудыг ашиглан А матрицыг байгуулна.

A = U*D*V";

А матрицын нөхцөлийн дугаар нь D матрицын нөхцөлийн дугаартай давхцах бөгөөд энэ нь бидний жишээнд 10 10-тай тэнцүү байна.

Бета = 1; гамма = 1e-5;

b" ба δb" векторуудыг бүтээх

B1 = "; db1 = ";

үүнээс бид b ба δb векторуудыг олно

X = A\b; x_tilda = A\(b+db);

тэгш бус байдлын зүүн ба баруун талыг тооцоол

dx = x - x_tilda; БАРУУН = норм(дб)/норм(б); ЗҮҮН = норм(dx)/норм(x);

мөн тэднийг гаргаж ир

Short e disp() форматлах

Бид тэгш байдлыг олж авдаг

1. Командын цонх(Тушаалын цонх).

Математик илэрхийллүүд нь командын мөрөнд " >> " мөрийн дараа бичигддэг. Жишээлбэл,

Үйлдлийг гүйцэтгэхийн тулд "Enter" товчийг дарна уу.

Анхдагчаар програм нь үр дүнг ans тусгай хувьсагч руу бичдэг.

Үр дүнг өөр нэрээр хадгалахын тулд хувьсагчийн нэр болон "=" гэсэн тэмдэглэгээг ашиглана уу

>> z = 1.25 /3.11

Засварлах Тушаалын цонхТа зөвхөн одоогийн командын мөрийг ашиглаж болно. Өмнө нь оруулсан командыг засварлахын тулд та курсороо оруулах мөрөнд байрлуулж, " " эсвэл " " товчлууруудыг ашиглах хэрэгтэй.

Хэрэв тушаал ";" -ээр төгссөн бол үйлдлийн үр дүн тушаалын мөрөнд харагдахгүй.

Командын цонхыг “ ” товчлуураар хааж болох ба “ ” товчлуур нь цонхыг системийн интерфейсээс салгахад үйлчилнэ. Та цэсийг ашиглан стандарт цонхны хэлбэрт буцаж болно.

Үндсэн цэс → Ширээний компьютер → Desktop Layout → Өгөгдмөл.

Та цэсийг ашиглан тушаалын цонхыг цэвэрлэж болно:

Үндсэн цэс → Засварлах → Командын цонхыг арилгах.

MatLab системийн үндсэн цэс.

Үндсэн цэс MatLabдараах зүйлсийг агуулна.

Файл(Файл) - файлуудтай ажиллах;

Засварлах(Засварлах) - засварлах;

Харах(Харах) - цонхны менежмент;

Вэб– интернетээр дамжуулан хөгжүүлэгч компанитай харилцах;

Цонх(Цонх) - системийн цонхтой холболт;

Туслаач(Тусламж) - тусламжийн системийн холбоос MatLab.

MATLAB системийн хэрэгслийн самбар.

Хэрэгслийн самбарын товчлуурууд нь дараах зорилготой.

Шинэ файл(Шинэ) – файл засварлагч цонхыг харуулна;

Файлыг нээх(Нээлттэй) - файл татаж авах цонхыг нээнэ;

Таслах(Cut) – сонгосон фрагментийг хайчилж, санах ойн самбар дээр байрлуулна;

Хуулбарлах(Хуулбарлах) – сонгосон фрагментийг санах ойд хуулна;

Буулгах(Paste) – сонгосон фрагментийг санах ойноос оролтын мөрөнд шилжүүлнэ;

Буцаах(Цуцлах) - өмнөх үйлдлийн үр дүнг цуцална;

Дахин хий(Дахин давтах) - өмнөх үйлдлийн үр дүнг давтах;

Simulink– Simulink загварыг бий болгодог (өргөтгөлүүд MatLab);

Тусламжийн цонх(Тусламж) - тусламжийн цонхыг нээнэ.

4. Тооцооллын үр дүнгийн гаралтын хэлбэр .

Бодит тоо оруулахдаа бутархай хэсгийг салгахад цэг ашиглана!

>> s = 0.3467819

Тооцооллын үр дүнг форматаар харуулна богино(тооны богино тэмдэглэгээ) нь анхдагчаар тодорхойлогддог. Та форматыг өөрчлөх боломжтой урт(урт тооны тэмдэглэгээ).

>> урт форматтай

0.34678190000000

Жагсаалтад Тоон форматтоон форматыг ашиглах боломжтой

богино- тооны товч тэмдэглэгээ;

урт- урт тооны тэмдэглэгээ;

богино e– хөвөгч цэгийн форматтай тооны богино тэмдэглэгээ;

урт e– хөвөгч цэгийн форматтай тооны урт бичлэг;

богино г– тооны богино тэмдэглэгээний хоёр дахь хэлбэр;

урт г– тооны урт тэмдэглэгээний хоёр дахь хэлбэр;

Цэсээс тоон өгөгдлийг харуулах форматыг тохируулж болно Файл(файл) зүйл Сонголтууд(сонголт). Таб руу оч Тушаалын цонх(тушаалын цонх). Сонголтонд Текст дэлгэц(текст дэлгэц), жагсаалтад байна Тоон формат(тоон формат) багц богино г, сонголтоор Тоон дэлгэц(тоонуудыг харуулах) тохируулна авсаархан. Эдгээр гаралтын форматууд нь таван чухал цифрээс бүрдэх бүх нийтийн хэлбэрээр тоог гаргаж, мөр хоорондын зайг дардаг.

MatLab дахь тооцооллын үндэс.

Энгийн арифметик үйлдлүүдийг хийх MatLabоператоруудыг ашигладаг:

· нэмэх хасах үйлдэл +, – ;

· үржүүлэх, хуваах *, / ;

· илтгэгч ^ .

Зарим тусгай хувьсагч:

ans - даалгавар тэмдэггүй сүүлчийн үйлдлийн үр дүн;

eps – хөвөгч цэгийн тооцооны харьцангуй алдаа;

pi - тоо;

i эсвэл j - төсөөллийн нэгж;

Inf - хязгааргүй байдал;

NaN – тодорхойгүй утга.

Зарим үндсэн суурь функцуудMatLab:

exp(x) – x тооны илтгэгч;

log(x) – х тооны натурал логарифм;

sqrt(x) – х тооны квадрат язгуур;

abs(x) – х тооны модуль;

sin(x), cos(x), tan(x), cot(x) – х тооны синус, косинус, тангенс, котангенс;

asin(x), acos(x), atan(x), acot(x) – арксин, арккосин, арктангенс, х тооны арккотангенс;

sec(x), csc(x) – секант, х тооны косекант;

round(x) – x тоог хамгийн ойрын бүхэл тоо хүртэл дугуйлах;

mod(x,y) – тэмдгийг харгалзан х-ийн y-д бүхэл тоон хуваалтын үлдэгдэл;

sign(x) – x тооны тэмдгийг буцаана.

Илэрхийллийн утгыг тооцоолъё

>> exp(–2.5)*log(11.3)^0.3 – sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))

Хэрэв операторыг нэг мөрөнд байрлуулах боломжгүй бол эхний мөрний төгсгөлд "..." гэсэн үргэлжилсэн тэмдгийг зааж өгвөл дараагийн мөрөнд үргэлжлүүлэн оруулах боломжтой, жишээлбэл,

>> exp(–2.5)*log(11.3)^0.3 – ...

sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))

Комплекс тоотой ажиллах функцууд:

Комплекс тоо оруулж байна

>> z = 3 + 4i

3.0000 + 4.0000i

abs(z), өнцөг(z) функцууд нь комплекс тооны модуль болон аргументыг буцаана, энд , ;

комплекс(a,b) нь түүний бодит болон төсөөллийн хэсгүүдээс цогц тоог бүтээдэг.

conj(z)комплекс коньюгат тоог буцаана;

imag(z), real(z) нь z цогцолбор тооны төсөөлөл болон бодит хэсгийг буцаана.

6. Векторууд.

Тоогоор оруулах, нэмэх, хасах, үржүүлэх.

Вектор дотор MatLabдөрвөлжин хаалт оператор ашиглан үүсгэсэн. Энэ тохиолдолд баганын векторын элементүүдийг цэг таслалаар “;”, мөрийн векторын элементүүдийг “” эсвэл таслалаар “,” тусгаарлана.

Баганын векторыг танилцуулъя.

>> x =

Мөрийн векторыг танилцуулъя .

>> y =

Векторыг шилжүүлэхийн тулд "'" апострофыг ашиглана:

>> z = y’

Векторуудын нийлбэр ба зөрүүг олохын тулд "+" ба "-" тэмдгийг ашиглана уу.

>> c = x + z

Векторыг тоогоор үржүүлэх нь "*" тэмдгийг ашиглан баруун болон зүүн талд хоёуланд нь хийгддэг.

Векторууд нь суурилуулсан функцүүдийн аргумент байж болно, жишээлбэл.

>> d = нүгэл (в)

Векторын элементүүдэд хандахын тулд хаалт () ашиглана, жишээлбэл,

>> x_2 = x(2)

Векторын сүүлчийн элементийг командыг бичиж сонгож болно

>> X_end = x(төгсгөл)

Жишээлбэл, хэд хэдэн векторуудаас нэгийг нь хийж болно

>> r =

1.3 5.4 6.9 7.1 3.5 8.2

Хоёр цэгийн тэмдэгт " : " нь олон элементийг вектороос салгахад хэрэглэгддэг

>> w = r(3:5)

Хоёр цэгийн тэмдэгт " : " нь мөн векторын элементүүдийг орлуулах боломжийг олгодог, жишээлбэл,

>> r(3:5)= 0

1.3 5.4 0 0 0 8.2

“:” тэмдгийг мөн вектор байгуулахад ашиглаж болох бөгөөд элемент бүр нь өмнөхөөсөө тогтмол тоогоор ялгаатай, өөрөөр хэлбэл. жишээ нь алхам

>> h =

1 1.2 1.4 1.6 1.8 2

Алхам нь сөрөг байж болно (энэ тохиолдолд эхлэлийн тоо нь эцсийн тооноос их байх ёстой).

Нэгтэй тэнцэх алхамыг орхигдуулж болно

>> k =

Векторуудтай ажиллах үндсэн функцууд.

• long(x) – x векторын уртыг тодорхойлох;
• prod(x) – x векторын бүх элементүүдийг үржүүлэх;
• нийлбэр(х) – х векторын бүх элементүүдийн нийлбэр;
• max(x) – х векторын хамгийн их элементийг олох;
• min(x) – х векторын хамгийн бага элементийг олох.

Хэрэв та min эсвэл max функцийг хоёр гаралтын аргументаар дуудвал = min(x),

дараа нь эхний хувьсагчд хамгийн бага (хамгийн их) элементийн утгыг, хоёр дахь хувьсагчд энэ элементийн дугаарыг өгнө.

7 матриц.

Төрөл бүрийн матриц оруулах аргууд.

1. Матрицыг хоёр элементээс бүрдэх баганын вектор хэлбэрээр оруулж болно, тус бүр нь мөрийн вектор бөгөөд цэг таслалаар тусгаарлагдана. Жишээлбэл, матрицыг танилцуулъя

>> A =

2. Матрицыг дараах тушаалуудын дарааллаар мөр мөрөөр оруулж болно.

>> A =)